Hook: (5-10 minutes, slides 2-4)

There are two options for a hook to choose from.  The hook intends to catch students’ attention onto the topic for the day, similar to a do now.  Both options prompt students to think about the proof of Pythagorean’s theorem which uses the area of the squares attached to each side.  Even if students do not fully conceptualize this proof after completing the hook, it is okay.  The hook just prompts students to begin thinking more deeply.  In both options the students engage in the notice and wonder protocol to give space for students to begin thinking about this proof of pythagorean’s theorem. Students will write their own things they notice and wonder about the video.  It is important to reinforce that there is no wrong answer – any idea they have is valuable.  Ideally students are given a few minutes of independent thought time to gather their thoughts.  In small groups 1 student shares 1 idea, then they go in a circle each sharing 1 idea.  Students then keep sharing ideas until everything they notice and wonder has been expressed.  It is important to share with students that they should share ideas even if they are repeated so they see what information consistently stands out.  Ideally students will begin to think more deeply about Pythagorean’s theorem than just a formula.  The goal is not for students to fully understand the proof yet, just to get them thinking.  

• Option 1 (slide 3):  Students are asked to watch a youtube video that shows water filling up the squares with width equal to the length of the legs of a right triangle.  When a device is turned the water then flows into the area of the square attached to the hypotenuse of the right triangle – it fills it up perfectly.  While watching this students engage in the notice and wonder protocol.  
• Option 2 (slide 4):  Students will complete the notice and wonder protocol about an image that shows the area of the squares attached to the legs of the triangle sum to the area of the square attached to the length of the hypotenuse.  This image uses more of a formula visual rather than a demonstration.  

Mathematical Exploration: (15-20 minutes; slides 5-11):

There are multiple ways for students to engage with Pythagorean’s theorem.  If you feel students have a solid understanding of Pythagorean’s theorem you can always skip the mathematical exploration and move onto the relevance explored.

The suggested activity hopes for students to continue to think about the proof of Pythagorean’s theorem so they can engage with it differently than they probably have in the past.  However, depending on your students’ needs and positionality this exploration can always be adjusted to be a more straightforward lesson about the formula and how to solve basic problems.  There are many lessons and options about students interacting with Pythagorean’s Theorem, use what works best for you.  

The suggested lesson provides an activity adopted by Jeong Oak Yun and Alfiino Flores that we have had success in our classes with.  The full research article and publication of this activity can be seen on the attached link on slide 6.  It is very similar to the do now and physically allows students to engage with this proof hands on.  The activity uses jelly beans to show how the areas of the squares attached to the sides relate to each other..  This time students will be able to physically move the areas to see how they compare:

• Set Up: (slide 7). This activity requires you to create a mat similar to the ones shown in the image.  It helps to print a base image like this:

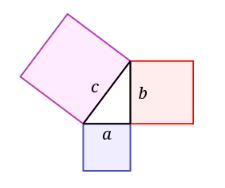
Then use cardboard to create “mini walls” on the perimeter of the image.  We have had the most success when gluing them with a hot glue gun.  Then have students fill up the blue and red squares with jelly beans to cover as much space as possible.  

• Explore (slide 8).  Students will then be asked to move the jelly beans around and see what conclusion they can make about the jelly beans.  After the do now students typically try to see if the same pattern follows.  If not, guide them to see how they can relate what they saw in the do now to this activity. 
• Conclusion (slide 9).  Students will discuss how this activity relates to Pythagorean’s theorem.  It is essential to use students’ ideas and discoveries to make an explicit connection to the mathematical theorem.  
• Extra Support (slide 10).  If students are struggling to see how the jelly beans can fill the areas there is a video demonstration that will visually show students how to complete the activity.
• Discussion (slide 11): The goal of this slide is to have students discuss the importance of understanding mathematical proofs.  Often students do not consider how mathematics was studied and developed.  Help guide students to think about mathematical contributions.  Additionally, the questions encourage students to think about receiving credit and being recognized for discoveries.  These questions  begin preparing them for relevance explored in receiving credit for mathematical findings.

If you feel students need a more tangible way to see how the areas sum to one another you can always explore this starburst activity shared on Mrs. Casia’s Math Blog: http://mrscasiasmath.blogspot.com/2020/07/introducing-pythagorean-theorem-with.html

Relevance Explored: (30-40 minutes; slides 13-26)

This part of the lesson transitions to thinking about inequities related to erasing the contributions from people of color to mathematics.  Historically, Pythagorean’s theorem was being used in civilizations for many years before Pythagoras even began studying mathematics.  However, the theorem is attached to his name.  To learn about this concept students will watch a cartoon video about how Pythagoras did not discover the theorem on slide 13.

To give students even more of a context for the community of followers Pythagoras had, have students read slide 14 as a class.  Often students do not understand that mathematical discoveries were such an important part of societies that they even had followers.  This should help students think about the personal benefits Pythagoras might have had to receive credit for mathematical contributions.  

We then transition to thinking about different civilizations’ discoveries and use the Pytahgorean’s theorem (slides 15-25).  Students will be given the chance to explore 5 different civilizations/locations that used Pythagorean’s theorem before Pythagoras. There are 2 suggested options for how students can meet this goal. 

• Option 1 (shorter): Each group receives a civilization and reads just the summary slides.  Have students discuss how this civilization used Pythagorean’s theorem.  Then have one student from each group share aloud in a whole class discussion their context.
• Option 2 (longer): Jigsaw – Each group will read their civilization’s summary and do additional research based on the additional resources slide.  Given each group he chance to explore and summarize their findings.  Then have students do a jigsaw share out in a small group where there is a representative from each group to share about the purpose of their textile patterns.

If you want to give students the chance to conceptualize further Pythagorean’s role in taking credit, students can watch the comedic dramatization of this history on slide 26.

Student Discussion: (10-20 minutes; slides 34-35)

The discussion questions intend to give students the space to process and discuss the connections between mathematics, proofs, miscrediting concepts and power/privilege.  The questions provided are just suggested questions and should be edited and developed to meet the needs, identities and personalities of your students.  They can be considered in partners, small groups or whole class discussions based on your student population.

Extension Activities: (slides 29-32) 

The extension activities are just opportunities for you and your students to explore options beyond what we have provided.  The possible extensions are not limited to what we have suggested.  There are many other extensions that could be created based on research you and your students can conduct.

• Extension 1: (slide 30)  Did we really prove Pythagorean’s theorem? Students can explore how rearranging areas can provide a new lens to proving Pythagorean’s theorem
• Extension 2: (slide 31)  Students can extend Pythagorean’s theorem to using semi circles instead of squares.  You can even pose students with the question – what other shapes can the theorem hold true with?
• Extension 3: (slide 32)  Students can watch a video contemplating if Pythagoras was a cult leader.